Monthly Archives: March 2019

Whole Body Air Displacement Plethysmographic- Problem

Posted on by

PROBLEM

In order for whole body air displacement plethysmographic machines such as the BodPod to function optimally (so that viable data can be collected), it is crucial that laminar flow is maintained throughout the machine’s ventilation system at all times. Imagine that you are an engineer (imagine that!)  tasked with manufacturing the tube components for the Bod Pod.

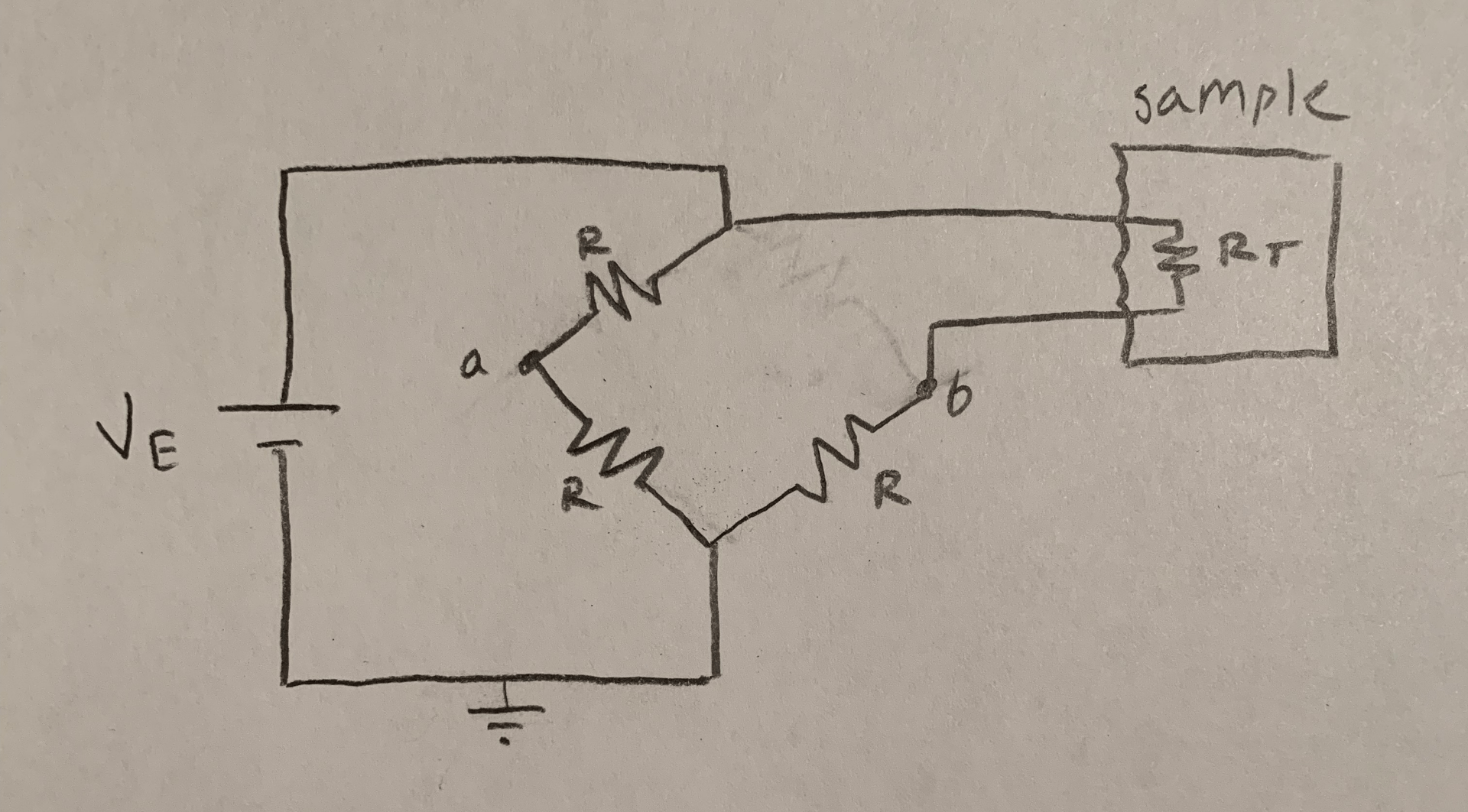
If the flow rates in the inlet and outlet tubes are equal, the volumetric  flow rate of air in the tubing system will be 0.25 cubic meters/second , and the BodPod functions in laminar/laminar-like conditions, what are the ideal dimensions for the diameters of the inlet and outlet tubes in the Bod Pod?

 

Assumptions

  • Flow rates are equal in the inlet and outlet tubes
  • The tubes are cylindrical  
  • Laminar flow is maintained at all times
  • Pressure changes are negligible
  • Air circulating inside the BodPod has similar thermodynamic/kinematic properties ambient air at room temperature
  • Temperature conditions of the device are identical to those at room-temperature

A link has been included to a power point presentation that contains diagrams that will aid readers in solving this problem:

https://docs.google.com/presentation/d/178RDbb09Vjwv3o7JVS9bkwR1TMjgWWApOBE5WDRzaQE/edit#slide=id.p

 

 

Figure 1: Schematic of Adult-Sized Bod Pod and circuitry components that will be used as a reference for this problem.

 

 

 

BACKGROUND KNOWLEDGE/ ASSUMPTIONS

According to the 4th page of the patent filed by the manufacturer, Life Instruments Inc., it is okay to assume laminar conditions inside the tubing ventilation due to the fact that flow rate inside the inlet and outlet tubes are always set to values of low magnitudes. Literature in courses such as Signals and Systems show that low flow rates result in low generation of acoustic noise by  air circulation systems.

 

I was unsuccessful in locating some sort of testing standard that establishes set values for the volumetric flow rates of air in laminar conditions. There appears to be any information pertaining to any testing protocols the manufacturer used for design verification purposes in the original 510(k) form filed with the FDA. To establish an appropriate flow rate value for this test question, I searched for similar problems online. In short, the values for the volumetric flow rate of air (Q) ranged from 0.1 to 0.8 cubic meters/second in my searches. I decided to use a value of 0.25 cubic meters/second in this problem. By assuming that the values for Q are equal for both tubes, it is possible to design both tubes with an equal diameter. Thus, along with other reasons that will be outlined later in this section, all the solver is required to do to calculate the correct value in this problem is to use one equation.

Normally, pressure fluctuations trigger changes in tubings and pipes create flow gradients in closed ventilation systems. Because of this, mathematical expressions such a Boyle’s Law and Bernoulli’s equations are used to solve changes in volume and volumetric flow when pressure fluctuations occur. According to page 4 of the patent filed for the Bod Pod, the authors state that the use of pressure transducers which are coupled to the inlet and outlet tubes helps monitor any pressure changes that occurs in the tubing; automatically adjusting the pressure settings in the tubes to more optimal levels through negative feedback. This is done in order to maintain a constant flow rate (and thus, laminar flow throughout the circulation system). Later on in section 4 of the patent,  the manufacturers also state that constant air flow can be maintained with the addition of rotary pumps to the circulation system (which are not actively displayed in any of the figures included).

The manufacturer’s statements in the patent confirm the presence of temperature-sensing circuitry in the inlet and outlet tubes that control the internal temperature of the environment inside the tubing and the pod itself. Thus, any temperature fluctuations that could create flow gradients in the device’s tubing are negligible since they are always corrected in  rapid fashion. This also eliminates the need for Fourier’s law to solve the value of Q in this problem.

Assuming that the tubing is cylindrical eliminates the need to solve for any hydrodynamic radius  values(which are used in equations associated with fluid flow in which tubes/pipes are any shape that is non-cylindrical).

 

By assuming that the air inside the device’s circulation system behaves in a similar fashion to ambient air, and that the conditions inside the circulation system are similar to those at room-temperature and that the device is used in STP conditions, it is possible to estimate the value of the kinematic viscosity of air (which is needed to solve the value for the diameter of the tubing using the Reynolds number equation along with the value of the flow rate given in the problem description and the upper-limit value of the Reynolds number associated with laminar flow).

 

SOLUTION

 

In order to solve for the value of the tube diameter, the solver must utilize the following equation:

Re = QD/v ,

Re = reynolds number

Q = volumetric flow rate of air

D = pipe bore or tube diameter

v = kinematic viscosity

Reynolds number flow rate equation-16umdck  <— Click the link to view a more detailed image of the equation

 

NOTE: Pipe bore is equivalent to the diameter of the tube, and this equation is applicable to both pipe and duct installations.

First, the value of Q is already provided in the description. So the reader is already provided one unknown.

Second, the reader is told in the problem description and background section to assume laminar conditions in the circulation system. The Reynolds number value used in this problem is 2300, which is the established upper limit for laminar flow. All values at or below this number is considered laminar flow.

Third, since the reader is told to assume that the air circulating through the inlet and outlet tubes are similar in kinematic/thermodynamic behavior to ambient air at room temperature, the reader can assume that air inside the circulation system has the same kinematic viscosity as ambient air at room temperature. This value is 1.494 x 10-5 meters ^2/ second.

At this point, the only unknown that the reader is left with is the value of D, or the tube diameter. After plugging all the known values into the above-aforementioned equation and solving for the value of D algebraically, the reader should arrive at a diameter value of approximately  0.13708 meters.

 

REFERENCES

 

[1] Dempster Phillip, Michael Homer, and Mark Lowe (2004). United States Patent 20040193074A1. Retrieved from https://patentimages.storage.googleapis.com/93/cf/ea/6d2d1346ea1129/US20040193074A1.pdf

 

[2] Engineers Edge. “Kinematic Viscosity Table Chart of Liquids” (2019). Machinery’s Handbook, 29th edition.  Retrieved from

https://www.engineersedge.com/fluid_flow/kinematic-viscosity-table.htm

 

[3] Foster, Trevon. “Laboratory Flow Meters: Flow Measurements In the Lab” (2015). Titan Enterprises, Ltd. Retrieved from

 

https://www.flowmeters.co.uk/laboratory-flow-meters-flow-measurement-in-the-lab/

Resistance Temperature Detector Calibration for Sweat Sensors

Posted on by

Glucose and Lactate are two analytes in sweat that would be highly desirable to apply sweat sensing technology to, each for their own individual reasons. Since the biosensing technology typically used to detect these analytes utilizes enzymatic reactions, temperature of the sample being tested must be taken into consideration when interpreting results due to its effects on enzymatic activity. Therefore, temperature sensors are an essential component of any sweat sensor that aims to give reliable feedback on either/both of these analytes. Multiple temperature sensing technologies exist, but a simple, commonly used technology is resistance temperature detectors (RTDs). These simple circuits use a Wheatstone bridge with a pure metal resistor that is exposed to the sample being tested. That resistor has a temperature-dependent resistance, and its resistance affects the voltage output of the Wheatstone bridge. In order to calibrate your sensor (a necessary process to ensure it gives accurate results), you must be able to use voltage outputs of known temperatures to identify the relationship between voltage and temperature. This problem will help us learn to do so.

 

Problem Statement

The Wheatstone bridge shown below (figure 2.) has four resistors, three of equal resistance R=10Ω and one temperature-varying platinum resistor RT. A voltage VE=1V is provided to the system by a battery as shown. Vo is defined as the voltage difference between points a and b, and is given by the general Wheatstone bridge equation provided below (figure 1.). Resistance RT is given by RT = R0(1+α(T-T0), where α is the temperature coefficient of platinum, α= 0.00385/°C. Given that R0= 10Ω and T0=0°C…

a. Write an equation for Vo in terms of T

b. Find Vo at T=20°C, T=30°C, and T=40°C

c. Devices aren’t always exact. Your RTD is giving values of Vo(20)=19.0mV, Vo(30)=28.3mV, and Vo(40)=37.2mV. Plot these values and find a line of best fit for your RTD (assuming linear relationship*)

d. Find the voltage Vo that would be expected at T=37°C

Figure 1. Wheatstone bridge equation

Figure 2. RTD setup

*Assumptions:

  • Linear relationship between Vo and T- RTDs display much more linear behavior than thermocouples. They are not exactly linear, but for the purposes of this problem and learning how to calibrate, it is a fair assumption. It will cause the most error in the middle of our range of estimation, due to the parabolic nonlinearity of the true relationship between Vo and T. [1]

 

Solution

Figure 3. The written solutions for a, b, and d

Figure 4. Plot for part c

The algebra for solutions to parts a, b, and d of the problem are provided in figure 3. The plot for part c, created in Excel, is provided in figure 4. This plot was created by creating a column of temperature data and a column of the corresponding voltage data given in the problem statement for part c, highlighting those two columns, and creating a scatter plot. A line of best fit was added to the plot, and the equation for the line was displayed on the graph itself. Excel makes linear approximations for data sets like these very easy. While the linear approximation may not be the best fit for our data set, it appears to be very accurate, with an R2 value of 0.9998. Our final answer for Vo at 37°C makes sense, given that 34.45mV is between the values for 30°C and 40°C, 28.3mV  and 37.2mV, respectively, and closer to that of 40°C. The linear approximation we made is a limitation of this solution. For a sweat sensing technology that gives medically relevant feedback to the user, we would want our analyte sensing results to be as accurate as possible, which would involve a curve-fitting technique as opposed to a linear approximation for our RTD. With the linear calibration we performed, we could use the values of Vo received from our RTD to determine the temperature of samples between 20-40°C with a pretty high level of accuracy.

 

 

References

[1] Trump, B. (2011). Analog linearization of resistance temperature detectors. Retrieved from http://www.ti.com/analog-circuit/aaj-article.html

One, Two Step

Posted on by

Wrist pedometers are used by many to count their steps, and notify users when they “reach their 10,000”. These wearable devices quantify step activity and give indiviudals an idea of exactly how much they are moving throughout the day.

Accelerometers are often used within these wearable devices to detect the force acting on the device. The force acting on the accelerometer is correlated to an analog voltage output, which must be processed through a series of op amps to turn a users movement into an electrical output that can be analyzed through signal processing, but what signal processing circuitry is needed following the accelerometer within a wrist pedometer to correlate force acting on the pedometer to steps taken by the user?

In this post we will solve at the following engineering problem associated with pedometers: what signal processing circuitry is needed to convert the analog voltage input from an accelerometer to a binary digital signal that can be correlated to steps taken by a user?

Background 

Figure 1. Force acting on wrist pedometer during gait cycle[1].

The average person takes between 0 and 120 steps per a minute. Throughout each gait cycle, a wrist pedometer experiences forces relative to its position, as shown in Figure 1. While standing the force detected by the pedometer is 1G (one times the force of gravity). When a user is pushing against the ground to step forward the force detected by the pedometer can rise above 1G, and while the user is between steps the force detected by the pedometer can go below 1G. The pedometer can detect when a user takes a step by monitoring forces and determining when the 1G threshold is crossed. Many wrist pedometers use a threshold of at least +/- 0.2G to prevent noise and standing movements from being accounted for in step count. So a step count will be equal to crossing the 1.2G and -1.2G thresholds[1].

 

Figure 2. Voltage Output as a function of force for Analog Devices+/- 2g accelerometer [2]

Accelerometers are often used to relate the force acting on an object to an electrical signal. Analog Devices, a circuitry component manufacturer, produces an +/- 2g accelerometer that relates forces between -2g and +2g to a voltage output, as shown in Figure 2. A linear region exists between +/- 2g, which can be defined by the following simplified function V(g)=(.875*g)+2.5 [2].

Approach 

In designing the signal processing circuitry necessary to convert an analog signal from an accelerometer to a binary digital signal, we will do the following:

1.Define the input signal in terms of force acting on a wrist pedometer, and the voltage output of an accelerometer

2.Determine the signal processing necessary to convert the analog signal into binary digital output

3.Select circuit components to complete desired signal processing, and appropriate values for integrated components

4.Use LTSpice to model desired circuitry, and confirm that designed circuit solves the defined engineering problem

Signal Input

It is known that the force acting on a wrist pedometer can be defined by a sine wave function fluctuating +/ 0.5g around 1g, with a frequency of 0-2Hz. Therefore we will define the force acting on the pedometer as F(t)= 0.5sin(t) + 1g. Given the voltage output of analog devices accelerometer is V(g)=(.875*g)+2.5, the voltage output of the accelerometer can be defined as V(t)=0.4105sin(t)+3.375.

Figure 3. Force acting on pedometer throughout gait cycle

Figure 4. Voltage signal generated by accelerometer from force input signal

 

 

 

 

 

 

 

 

Signal Processing

To generate a digital binary signal from an analog voltage input signal processing through circuitry is required.

Figure 5. Flow chart of signal processing of input analog signal from accelerometer to binary output signal

First, the input signal should be passed through a low pass filter, with a cutoff frequency of 2Hz to remove high frequency noise from the signal. The force acting on the pedometer, and voltage output of an accelerometer can be defined by sine wave functions. The baseline of accelerometer voltage output exists above zero volts, therefore a subtractor should be used to bring the baseline of this signal to 0V. A full wave rectifier will be used as an AC to DC converter, converting both polarities of the signal to a pulsating DC signal. A compactor will be used to produce a binary DC output that indicates whether the signal is above a given threshold, voltage relative to passing +/- 0.2g force threshold. This binary signal is the system output and can be used to count total steps taken by a user.

Circuit Components 

Circuit components were selected to complete necessary signal processing, and assumed to be ideal for simplification of solving this problem.

Low pass filter 

Figure 6. Low pass filter

 

With a cutoff frequency of 2Hz, a low pass filter with a Capacitor of 4.7 nF and resistor of 0.0169 Ohms can be used to filter out high frequency noise

 

 

 

 

Follower

Figure 7. Op amp acting as follower

 

Follower used to preserve signal and prevent current flow back to the user

 

 

Subtractor 

Figure 8. Op amp acting as a subtractor

 

A subtractor can be used to reduce the baseline signal to zero. Given our voltage input is V(t)=0.4105sin(t)+3.375 V, and the Voltage output of this component is Vout = (R3/R1)*(Vin-Vs), we will set Vs=3.375V DC and R1=R2=R3=100 Ohm to bring the baseline signal down to 0V.

 

 

 

 

Full Wave Rectifier

Figure 9. Op amps acting as a full wave rectifier

 

A full wave rectifier will be used to convert all polarities of the input signal to the same polarities. If R1=R2=R3=R4=R5, then if Vin>0 Vout=Vin and Vin<0 Vout=-Vin. Therefore, we will set all the resistors equal to each other to achieve a rectified DC signal.

 

 

 

Comparator 

Figure 10. Op Amp acting as a comparator

A comparator will be used to convert the pulsating DC signal to a binary digital output. Op amps functioning as comparators follow the rule that if V+>V- Vout = Vc+ and V->V+ Vout=Vc-. In our ideal circuit, we aim our binary signal to be either 0 or 1.

V+ terminal will be our signal, and we look to determine if this signal represents crossing the 1.2g threshold. To find what the V- terminal should be we need to determine the voltage at this point in the circuit if it has crossed the threshold. Given, V(g)=(.875*g)+2.5, V(g=1.2)=3.52. The signal is brought through a subtractor where it is reduced by 3.375 and afterword is no longer amplified or modified, so the threshold voltage at this point is 0.1534 V. The negative input terminal will be set to be a DC voltage of 0.1534V.

To generate a binary output where 0V= not crossing the threshold and 1V= crossing threshold, the op amp terminals will be set to be Vc+ = 1V and Vc-=0V.

LTSpice Modeling and Verification 

Figure 11. LTSpice signal processing circuit following accelerometer to convert analog accelerometer signal input to binary output


LTSpice was used to model the designed circuit, as shown in figure 11. This circuit was simulated using LTSpice software and it’s ability to produce a binary digital output from an analog signal was verified as depicted in figure 12.

Figure 12. Voltage input, green, and output, blue, of signal processing circuit in figure 11

Solution

Our goal was to design signal processing circuitry is needed to convert the analog voltage input from an accelerometer to a binary digital signal that can be correlated to steps taken by a user.

Figure 13. Accelerometer analog output signaling processing circuit to produce binary digital output

A series of signal processing components were integrated within a circuit, depicted in figure 13, to convert an analog voltage signal from an accelerometer into a binary digital signal. This circuit removes high frequency signal noise, reduces the signal baseline, generates a pulsating DC signal, and generates a binary signal output, as shown in figure 14.

Figure 14. Binary digital output of accelerometer signal processing circuit

This binary digital output can be correlated to steps taken, as two square waves is equal to one step taken. These square waves can be counted by an integrated software and used to count user steps. Thus, turning the analog accelerometer voltage output into a binary digital signal.

This binary signal can be used to count steps and step frequency, and when integrated with GPS and other technologies can be used to determine step distance and user speed.

With one two sqaure waves equaling a step, the designed integrated circuit turns user movement into step count, enabling the signal processing necessary to count those 10,000 steps everyone is so desperately trying to reach!

References

[1] Modi, Yash Rohit. (2014). United States Patent No. US20140074431A1. Retrieved from https://patents.google.com/patent/US20140074431A1/en

[2] “Accelerometer Specifications – Quick Definitions.” Accelerometer Specifications – Quick Definitions | Analog Devices, www.analog.com/en/products/landing-pages/001/accelerometer-specifications-definitions.html.

Isokinetic Dynamometry Engineering Problem

Posted on by

Isokinetic Dynamometry Engineering Problem:

An 18-year-old, 5’4”, 130 lbs female soccer player is just recovering from an ACL tear and wants to know if she can get back in the game. She has been super cautious and tentative to rehab strength exercising routines, so she is sure she is ready, but wants to quantify her strength. To do this, she decides to measure her quadricep and hamstring strength on an isokinetic dynamometer and evaluate her hamstring to quad ratio, which should be between 50 and 80 percent [1]. Other important values include power, work, and peak force to assess the muscle and plan for future rehab exercise routines.

Based on previous studies, to test for power and strength of a muscle, the optimal speed is 60º/sec [2]. She also performs the test with a range of 0-90 º. The results of her hamstring force came back as 54.663 lbs and her recorded quadricep torque value determined by the isokinetic dynamometer is 102.45 lbs*ft3. The patient also wants to know her kick velocity (for fun). The computer is not properly calculating important values, and hand calculations must be performed to ensure accuracy. Calculate the power, work, and force of the quadricep, the angular speed at which the leg kicks, and the hamstring to quadricep ratio to determine if the patient can go back to playing.

*See attached anthropometric weight and measurement documents to determine distance and mass

 

Solution:
Assumptions: To simplify the math, we are ignoring the effects of gravity and inertia from the swinging limb. In real life, they play a major part in the force read by the machine and there are algorithms the computer goes through to factor out the effects. Also, the math that is performed based on the free body diagram is the forces on the knee joint, not just the quadricep. There are many forces that play a part, but for simplicity reasons we will treat them as only the force produced by the quadricep. Furthermore, there are other considerations when thinking about ACL recovery such as muscle strength and also whether or not the muscles are even. In this problem, we only look at one muscle and do not do a comparison.

1.Since Torque is given (102.45 lbs*ft), Force can be found by

Torque=〖Force〗_quad x d or 〖Force〗_quad*d_perpendicular
First: find perpendicular distance, which will be the length from the patient’s knee to ankle (d on free body diagram)
From the anthropometric table, the distance is Height*(0.285-0.039), where H= 5.33 ft.
Therefore. d=1.312 ft

102.45 lb*ft=〖Force〗_quad*1.312ft
〖Force〗_quad=78.09 lbs

2.Now that Force of the quadricep is found, we can solve for work

The distance, in this case, is the distance the leg travels, which will be the arch distance
s (arch distance)=rθ
r in this case is equal to d. Also, the range (θ) is 90 º, which in radians is 1.571 (90*(π/180))
s=(1.312)(1.571)= 2.06 ft
Now that we have d, multiply by force to get work
Work=78.09 lbs*2.06 ft=160.96 ft*lbs

3.Power can be solved by using the equation

Power=torque*angular velocity
Angular velocity is 60º/sec, which in radians (multiplied by (π/180)) is 1.047 s-1
Plugging in,
Power=102.45lb*ft*1.047 s^(-1)=107.28 (ft*lb)/sec

4.To find angular velocity (ω) her leg is going, the angular acceleration must be determined based off of the force exerted by the quadricep

The following equations must be used
F=m_lowerleg*a_n
a_n=ω^2 r,where r=d
*Note: Since there is a circular motion, angular acceleration must be assessed. Since there is a constant velocity, there is no at component.

Using the weight chart, you should find the weight of the lower leg is 0.0618*weight, which in this case is

(0.0618*130 lbs)/(32.2 )=0.2495 s

Therefore:

78.09 lbs=0.2495 slugs* ω^2*1.047 ft
ω^2=298.7 rads/sec
ω=17.28 rads/sec (times 180/π to get degrees)
ω= 990.2 º/sec

5.Finally, to find hamstring to quadricep ratio

Ratio=(Hamstring Force)/(Quadricep Force) x100
Ratio=54.663/78.09 x100=70%
Therefore, it can be concluded the patient can return back to the field

Overall
Force (quad) = 78.09 lbs
Work=160.96 ft*lbs
Power=107.3 ft*lbs/sec
Angular Velocity = 990.2 º/sec
Hamstring/Quad ratio = 70%
All of these values make physiological sense and line up with average results from other research[3,4]

Tables

Figure 1: Mean Segment data taken from https://exrx.net/Kinesiology/Segments

 

Figure 2: Anthropometric data showing body segment length as a function of total height. From Winter, D.A., Biomechanics and Motor Control of Human Movement, Wiley Interscience, New York, 1990

Sources:

  1. Rosene, J., Fogarty, T., & Mahaffey, B. (201). Isokinetic Hamstrings:Quadriceps Ratios in Intercollegiate Athletes. Journal of Athletic Training,36(4), 378-383. Retrieved from https://www.ncbi.nlm.nih.gov/pmc/articles/PMC155432/pdf/attr_36_04_0378.pdf.
  2. Duarte, J. P., Valente-Dos-Santos, J., Coelho-E-Silva, M. J., Couto, P., Costa, D., Martinho, D., … Gonçalves, R. S. (2018). Reproducibility of isokinetic strength assessment of knee muscle actions in adult athletes: Torques and antagonist-agonist ratios derived at the same angle position. PloS one, 13(8), e0202261. doi:10.1371/journal.pone.0202261
  3. Holmes, & Alderink. (1984). Isokinetic Strength Characteristics of the Quadriceps Femoris and Hamstring Muscles in High School Students. Physical Therapy,64, 914-918. Retrieved from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1016.6759&rep=rep1&type=pdf
  4. Heyward, V.H. (2010) Advanced fitness assessment and exercise prescription (6th Ed.) Champaign IL: Human Kinetics

 

 

 

Engineering Concerns for a Portable NIRS Device

Posted on by

When designing a portable Near-Infrared Spectroscopy (NIRS) device for the measurement of muscle oxygenation, design engineers have plenty of factors to consider. They must think about battery life, portability, affordability, safety, and many other design criteria. Before considering many of these criteria, however, an engineer must design a working technology that is capable of actually measuring muscle oxygenation. Without this basic attribute, the device would be a complete failure. The basics for measurement of relative oxygenated and deoxygenated hemoglobin concentrations was introduced previously in the patent blog post, but the engineering design problem was mostly glossed over. This post will dive a little deeper into the quantitative nature of measurement of muscle oxygenation and what functions the design engineer must consider when designing a device that will operate properly and accurately. The main question to be answered is: how does an engineer use light to measure concentration of a particle in muscle?

Fig 1: Molecular Absorption Coefficient Profiles for Oxygenated and Deoxygenated Hemoglobin

As mentioned before, NIRS works by measuring the absorbance or attenuation of light as it passes through a sample to make a measurement of concentration of the absorbing analyte or particle. Also previously introduced were the benefits of using near-infrared light since it can pass through biological tissue and is primarily absorbed by hemoglobin. In an ideal world the absorbance is defined by the Beer-Lambert Law. According to this law, the absorbance of a particle is equal to the natural log of incident light over the detected light and this is further equal to the product of the molar absorbance coefficient, the concentration of the particle, and the mean path length of detected photons. In an ideal case this law works because it describes when light is shown through a glass cuvette with a solution with only one absorbance particle, but this is not helpful for a NIRS device for muscle oxygenation. Thus, for a NIRS device, the modified Beer-Lambert Law must be used, which is the same as the original equation but with an extra scattering term to account for photon scatter when passing through tissue like skin and muscle (Eqn. 1).

Here A is absorbance, I0 is incident (transmitted) light, I is detected light, ɛ is molar absorbance coefficient, c is concentration, L is mean path length, and G is the scattering term. This is great in theory because it appears that concentration can be calculated relatively easily, but there are further problems to solve. Start by considering the knowns and unknowns. The absorbance coefficient is a known value for any analyte given the wavelength of the laser used (Fig. 1), and the path length can easily be found from the distance between the light emitter and detector with some regards to the path shape which is known to be roughly banana shaped. This leaves two unknown terms: the unknown that to be measured, i.e. concentration, and the scatter term. The scatter term is unfortunately a problem. It varies by tissue and considering the device should be designed for consumers to use on different locations, different muscles, and different amounts of say fat that may lie in the way of the muscle, this G term will forever be changing. Thus, there needs to be a way to get rid of it. The easiest way to do this is to find change in absorbance so that G will be subtracted away. This uses the assumption that G is constant for a given location. The resulting equation will then give change in concentration as it is the only factor that changed between measurements 1 and 2 (usually an initial measurement and a second measure at a later time) (Eqn. 2). Notice that absorbance is now equal to the natural log of the first intensity detected divided by the second intensity measured based on the identity (log(x/y) = log(x)-log(y). Note that the need to get rid of G, because it cannot be calculated on every single consumer, leads to the fact that NIRS devices almost always measure change in concentration or relative concentration when measuring muscle oxygenation.

This equation looks great. So change in concentration as opposed to exact concentration is found, but so what, this is still a very helpful measure for oxygenation during exercise. BUT, this equation is not the whole story. NIRS works by measuring both oxygenated and deoxygenated hemoglobin (Hb). Both species of Hb contribute to absorbance in the near-infrared range. Thus the equation actually looks like this (Eqn. 3)

In this equation, subscript O is used for oxygenated Hb, and subscript Hb is used for deoxygenated Hb. Now there are two unknowns and only one equation. So what does a smart engineer do? They add more lights. By measuring multiple wavelengths, two changes in absorbance can be measured allowing both concentrations to be calculated by solving the system of equation (Eqn. 4-5).

In these equations, superscripts refer to the wavelengths of light 1 and 2. It must be remembered that absorbance coefficient, absorbance change, and path length will all vary based on wavelength. This clearly allows for the output of relative concentrations or total blood oxygen saturation percentage (oxyHb / [oxyHb + deoxyHb]). Here the assumption is that total Hb is equal to oxyHb plus deoxyHb. The last piece of the puzzle for an engineer is to decide on what wavelengths should be used for the lights. This is a very impactful decision in building the algorithm to calculate the outcome measures of the device since ɛ, A, and L all depend on wavelength. It should be noted based on Figure 1 that certain wavelengths will be better than others. For example, if 805 nm light is used, then the absorbance coefficients for both species of Hb will be the same. This leads to irrational answers for Equations 4 and 5, so this wavelength should be avoided. The best case is to pick a wavelength above and below this so that one is more sensitive to oxyHb and the other is more sensitive to deoxyHb. Thus, using 750 and 850nm could be viable options, and these are used in several current devices.

These results allow an engineer to design a device that will properly measure muscle oxygenation through the relative concentrations of oxygenated and deoxygenated Hb. A reminder that some of the assumptions that needed to be made were that the tissue was homogenous, that oxy and deoxy Hb are the only particles contributing to absorbance, that absorbance is constant in time when Hb concentrations do not change, that the scattering term remained constant, and that oxy + deoxy Hb is the total Hb. Realistically, tissue is not homogeneous, but this assumption causes smaller errors in the volumes being considered close to the skin surface. Unfortunately, Hb is not the only chromophore contributing to absorbance. Fat is a major problem because it shares a similar range of wavelengths for absorbance. Some devices take fat correction into account, but other do not, and papers have pointed this out. It is reasonable to assume that absorbance is constant in time when concentration is constant, but pulsatile flow can cause error here. The scattering term should remain constant if the position of the device is not changed, and it is also reasonable to assume that there are not Hb species besides oxy and deoxy in the muscle. Some of these do cause limitations to the design described here, and as already mentioned it will only measure change in concentration not the absolute value. In conclusion, two wavelengths of light are needed measure muscle oxygenation with NIRS.

 

References

[1]. Shimadzu Commercial Website https://www.ssi.shimadzu.com/products/imaging/labnirs-principle-of-operation.html

[2]. Kocsis, L., Herman, P., & Eke, A. (2006). The modified Beer-Lambert law revisited. Physics in Medicine and Biology, 51(5). http://doi.org/10.1088/0031-9155/51/5/N02

[3]. Len-Carrin, J., & Len-Domnguez, U. (2012). Functional Near-Infrared Spectroscopy (fNIRS): Principles and Neuroscientific Applications. Neuroimaging – Methods. http://doi.org/10.5772/23146

[4]. McManus, C. J., Collison, J., & Cooper, C. E. (2018). Performance comparison of the MOXY and PortaMon near-infrared spectroscopy muscle oximeters at rest and during exercise. Journal of Biomedical Optics, 23(01), 1. http://doi.org/10.1117/1.jbo.23.1.015007

Better Building: Making An Accurate Wearable

Posted on by

Identify:

Heart rate measurements are a very versatile and useful tool for both starting and veteran athletes. Among many other uses [1], it can be used as a general gauge of how hard you are working out at that moment, and it can help determine improvement as your max heart rate increases. But putting a hand to your chest and counting the beats per minute is an impractical way to measure heart rate. So to help us measure this useful metric, we have heart rate monitors that can take our heart rate for us.

On the market, there are two types of heart rate monitors: Chest-strap monitors and wrist-strap monitors. Most people who aren’t even athletes probably have a wearable that can monitor heartbeats. Even most modern phones have the ability to measure your heart beats. However, despite their ubiquity, they have one major downfall: Wrist-strap monitors simply aren’t incredibly accurate. Besides the point of location, the wrist has several different factors [2] that make it difficult to get a good reading, ranging from skin-tone to motion. All of these factors produce noise that helps to muddy the results and can produce odd and inaccurate readings. To ensure we get the most accurate results to accurately determine our exercise maximum, it is this noise that we must turn to curb. But how do we go about reducing noise?

Formulate:

Modern wearable HRMs use a technology called photoplethysmography or PPG. In essence [3], the device shines a light through a bulb (usually an LED), that passes through the skin and muscles. A majority of this light will be absorbed by the surrounding skin and muscles. The blood absorbs the light that does make it through, which is the crux. By measuring the amount of light that is absorbed, the device can pick up on pulses in the blood based upon the differences in these absorbances. This technology is very similar to how spectrophotometers work, with both measuring the absorbance that a material has. But unlike a spectrophotometer which measures the absorbance through the material, PPG measures constantly, listening in for very small changes in absorbance that can be used to determine heart rate.

An example of PPG. Pulses within the vessel cause even more light to be absorbed than would normally. This is what the wearable is measuring.

PPG is very sensitive to physical sensations like bumps and pumps, which produces noise. When the sensor is jostled due to motion, the small amount of signal that is recorded gets muddled, which produces the majority of the noise that we are trying to cut down. This noise can cause very odd results, such as heart rates that vary wildly [4]. The noise is not present while not in motion, but for athletes who want to know how high their heart rate can get, this is not acceptable. As noise caused by motion is the leading cause of these very odd discrepancies in heart rate, we need to lower it as much as possible.

In order to solve this, we are going to separate the signals read between three metrics: a DC, an AC, and a noise component. We shall be ignoring noise caused by the optical signal, as it is subtracted by the sensor through the use of ambient light measurements [5]. Thus, the incoming current that is read can be simplified as:

Incoming Current = DC component + AC component + Noise

The DC component of the signal comes from changes in respiration in the vessel, while the AC component comes from variation in blood volume due to the heartbeat.

Solve:

If we want to reduce the amount of noise, we are going to have to pass the incoming signal through a filter. When the signal comes back to the wearable, it must interpret the signal, from raw absorbance values to electrical signals that are then interpreted by the wearable. And since we assume that optical light noise is negligible, we can focus on removing noise due to motion. Using biophysical-signal characterization techniques [6] as our filter, we can compare the incoming signal, and remove noise caused by motion. The remaining non-noise components will have to be amplified in order to get a complete, accurate signal. We do this in order to fill in the gaps made when we remove several points of noisy data.

By using a current filter, we hope to minimize the amount of noise that is detected alongside the heart rate of the monitor. If we can eliminate the noise read alongside the signal, we can get more accurate results, as the signal interpreted would consist only of the AC and DC components. However, this approach focuses only on noise made by motion. As stated before, there are several different sources of noise that interfere with accurate measurements. While motion is one of the primary sources of noise, other factors like skin tone, gaps between the sensor and the skin, and the location of the sensor can introduce more noise. This solution also has the possibility of cutting off accurate readings that are interpreted by the sensor as noise. Athletes who do a lot of vigorous exercises may find that their heart rates are inaccurate under this solution if their heart rates spike hard enough during exercise.

[1]: Shmerling R. How’s your heart rate and why it matters? – Harvard Health. August. https://www.health.harvard.edu/heart-health/hows-your-heart-rate-and-why-it-matters. Published 2017.

[2]: LeBeouf S. Five Challenges of Optical Heart Rate Monitoring. Sensors online. https://www.sensorsmag.com/components/five-challenges-optical-heart-rate-monitoring. Published 2016.

[3]: Cheriyedath S. Photoplethysmography (PPG). News Medical Life Sciences. https://www.news-medical.net/health/Photoplethysmography-(PPG).aspx. Published 2016.

[4]: Oniani, Salome & Woolley, Sandra & Pires, Ivan & Garcia, Nuno & Collins, Tim & Ledger, Sean & Pandyan, Anand. (2018). Reliability Assessment of New and Updated Consumer-Grade Activity and Heart Rate Monitors. 10.13140/RG.2.2.35628.72328.

[5]: Wearables | OSRAM. https://www.osram.com/os/applications/mobile-competence/mobile_competence_wearables.jsp.

[6]: Maity S, He M, Nath M, Das D, Chatterjee B, Sen S. BioPhysical Modeling, Characterization and Optimization of Electro-Quasistatic Human Body Communication. IEEE Transactions on Biomedical Engineering. http://arxiv.org/abs/1805.05200. Published May 14, 2018.

Personalized BioElectrical Impedance Analyzer

Posted on by

Identify

 It is common for people worry about their Body Mass Index (BMI) values after visiting the doctor’s office. What many people don’t know is that these BMI values do not take into account what body weight comes from muscle and what comes from fat. This can be hard for individuals who contain high amounts of muscle, which weighs more than fat, and get a BMI value back saying that they are overweight.

One way to differentiate between an individual’s fat free mass (FFM) and their fat mass (
FM) is by using a bioelectrical impedance analyzer. These analyzers work by sending a low electrical current through the body from one electrode to another. This electrical current will pass quickly through hydrated tissues such as muscle and slowly through low hydrated tissues like fat.

                                                           

There are many different factors to be taken into consideration when programming a bioelectrical impedance analyzer as shown above. Many estimated values for these analyzers come from average values and standard deviations of measurements from more accurate body composition tests such as hydrostatic weighing or Dual-energy X-ray absorptiometry (DXA). Specific equations based off of these values must be input into the system that will be able to give back estimates of an individual’s specific body composition given an input of the individuals weight, height, and gender. The problem with these analyzers is that the estimated values don’t accurately or even closely relate to each individual.

 Formulate

For a bioelectrical impedance analyzer, the impedance value is mathematically found from the equation Z^2 = R^2 + Xc^2. Within this equation Z is the impedance, R is the resistance, and Xc is the reactance. The resistance is the opposition of a conductor to the alternating current and the reactance is the additional opposition to the current from the storage effects of the cell membranes and tissue interfaces.

As an engineer it is important to find the right programming equations for the technology being made. These equations will vary in accuracy depending on the sex and ethnicity of its user. After the impedance has been calculated from the electrical current, it will need to be plugged into an equation, along with height, weight, and gender to find fat mass. When using segmental analyzers each different segment being measured will use its own specific equations for FM and the segments will then be summed for a total body FM. A typical FM equation for a non-segmental analyzer for ages 16-80 may be set up as:

FM(kg) = C1 + C2 Age + W + C3 (H(m)^2 / Z) – C4 H(m)

Where H(m) is height in meters, W is weight kg, Age is age in years, Z is from the previous equation depending of the testing frequency and each C variable is a different constant. The constant values will be determined using linear regression models of data taken on a group of individuals using a different form of body composition analysis.

The following assumptions can be made when programming the equations:

  1. The electrical current follows the path of least resistance within the body
  2. Both the body and its specified segments follow a cylindrical ‘typical’ shape

If these two assumptions hold true and the following equations are programmed correctly an FM estimate can accurately be made.

 

Solve

 The following measurements and calculations will then be made for fat mass:

Z^2 = R^2 + Xc^2

FM(kg) = C1 + C2 Age + W + C3 (H(m)^2 / Z) – C4 H(m)

Using the standard deviations as C values from data taken from a previous body composition study in Japanese women [1],the following equation can be determined:

FM(kg) = 37.91 + 18 Age + W + 0.6144 (H(m)^2 / Z) – 6.7 H(m)

Using these calculations along with a weight measurement from a scale an individual can then accurately assess their body composition health and fat free mass rather than using the BMI percentile chart.

Weight = FFM + FM

FFM = Weight – FM

It is important to understand that this developed equation will be limited only to Japanese females. If a scale programmed to find fat mass using this equation was used by a male, even a Japanese male, they would get an inaccurate reading. These reading will be inaccurate mainly due to the differences in how each sex and different ethnicities hold water within their body. This equation found for a BIA scale would be reasonable for female Japanese users only. In order for the scale to be reasonable for other individuals the programmed equation will need to be changed based of previous body composition findings of other groups based on ethnicity and sex.

Further Readings:

 https://www.sciencedirect.com/science/article/pii/S0261561408000666?via%3Dihub

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4608267/#CR18

References:

 https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5551247/

 Image Sources

 https://www.valhallawellness.com/weight-loss-services/bioelectrical-impedance-analysis/

7 Minutes of Sweating: Taking the HIIT

Posted on by

One of the most commonly stated New Year’s Resolutions is losing some extra pounds, starting a jogging routine, or otherwise getting physically fit. It is a very noble goal with good intentions, but many people who make this resolution for the new year end up breaking this promise to themselves. Chief among the reasons for quitting is the lack of time during the day. Between work, school, family, friends, and other obligations, it can be hard to set aside one or two hours to do a full traditional workout routine. But what if there were a way to get some exercise in regardless? What if you could work out for as little as 7 minutes, and get the same results as if you worked the full hour? As long as you follow a specific type of workout, this dream could be a reality. Enter: High-intensity interval training.

Figure 1: A Warrior Training instructor, leading her class.

By Any Other Name:

High-intensity interval training (HIIT) takes many different forms and names: Tabata Training, Sprint Interval Training, 7 Minute Workouts, and Warrior Training are all different forms of HIIT. The core idea behind HIIT is that athletes who take part of these programs work at maximum exertion for a short period of time before taking a short break. According to the guidelines put forth in the ACSM’s Health & Fitness Journal [2], working at a maximal output for short bursts of time causes you to generate close to 90% of your VO2 Max (also known as a VO2 Peak) over the course of the exercise. These guidelines, which have formed the basis of the 7 Minute Workout, pen the program as a time-efficient way to get similar efforts to other workouts that last longer, by trading time for increased effort. But how true is this claim? Can you really get the same workout you would in an hour in the span of 7 minutes, simply by working at maximal output? This is the question, one that I hope to answer.

Insulin Activity:

One study [3] focused on the potential for Sprint Interval Training (SIT) to be used for promoting insulin sensitivity, as well as other indicators for increased cardiometabolic health. In this study, they took 27 sedentary men with similar age, weight, and VO2 Peak. These men were divided into three groups and were given different workout routines: one was SIT, one was a traditional moderate-intensity continuous training (MICT), and the last did not train at all as a control. The SIT group would do high intensity, 10-minute sessions, while the MICT group would do more moderate bouts over 50 minutes sessions. Over the span of 12 weeks, these men worked out and got measurements of their results. They concluded that SIT was comparable to MICT, with regards to improving VO2 Peak, insulin sensitivity, and skeletal muscle adaptations. The study does not, however, make any mention of weight loss, though that is due to it being outside of their scope.

Figure 2: VO2 Peaks of the different groups in the study before, in the middle of, and after the full study.

New Year’s Resolution Buster:

In regards to body fat, one review [4], though dismayed at the effort required to adhere to the HIIT program, found it to be a preferable alternative to MICT. In that review, not only did they find many of the same adaptations from the study above, they found that many studies point out increased levels of skeletal muscle fat oxidation using HIIT. Another study [5] found that HIIT, while better than sedentary activity, was not significantly better than MICT, and may even be slightly worse. Still another study review [6] suggests that HIIT and MICT have similar benefits, with the only difference between the two being time.

One term that gets thrown out a lot during discussions is EPOC or Excess Post-Exercise Oxygen Consumption. Long name aside, it is a process that your body undergoes after exercising in order to bring the body back to a normal state. In this recovery state, the body uses more energy and calories compared to your resting rate as it tries to help heal and build your muscles. This gets thrown around especially in regards to HIIT, as some review articles [6] report that HIIT can lead to increased levels of EPOC, compared to MICT. This sounds like a decisive point in HIIT’s favor, as calorie burn is often the biggest signifier of hard work for starting athletes. But the actual amount of calories that are burned as a result of EPOC, according to this review [7] might not be very substantial in the first place.

The Bottom Line:

Armed with all of this information, what can we say about HIIT? As a form of exercise, it seems to be a perfectly valid way of working out. Whether it is better or worse than traditional duration exercises is up for debate, but HIIT is at least around as good as MICT. Both MICT and HIIT cause similar increases in VO2 Max and other adaptations such as increased insulin sensitivity. Neither method has been shown to be significantly better at burning calories, either.

That being said, one common theme appears across several studies is how harsh the workout is. In almost every single review study involving HIIT, the discussion often concedes that HIIT is very intense and that not everyone will be able to maintain the level of exertion requested by HIIT. With this, I can say that HIIT will not be replacing MICT. Ultimately, the question of whether to do MICT or HIIT comes down to personal preference. If you don’t have time during your day and are willing to really sweat it out for a short amount of time, then HIIT is a good alternative choice. If you do have time during the day and don’t want to work out to near your maximal output, then stick with a more traditional workout may be the right thing for you.

Questions To Consider:
  • Given a choice between working out using the HIIT method or the traditional MICT method, which would you choose?
  • Would you recommend HIIT to a beginner athlete?
  • What about someone more grounded in their routine? Would you ask them to give it a shot?
  • Looking through a calories-down lens, would you focus on HIIT?
  • If you are working out using the traditional MICT method, would you integrate some HIIT workouts in there as well?
  • Given the short time investment, would you work out using HIIT 7 days a week?

[1]: Figure 1: Warrior Trained Fitness offers service members, families’ group workout. https://www.nellis.af.mil/News/Article/665186/warrior-trained-fitness-offers-service-members-families-group-workout/.

[2]: Klika B, Jordan C. HIGH-INTENSITY CIRCUIT TRAINING USING BODY WEIGHT. ACSMs Health Fit J. 2015;17(3):8-13. doi:10.1249/fit.0b013e31828cb1e8

[3]: Skelly LE, Martin BJ, Gibala MJ, Gillen JB, MacInnis MJ, Tarnopolsky MA. Twelve Weeks of Sprint Interval Training Improves Indices of Cardiometabolic Health Similar to Traditional Endurance Training despite a Five-Fold Lower Exercise Volume and Time Commitment. Sandbakk Ø, ed. PLoS One. 2016;11(4):e0154075. doi:10.1371/journal.pone.0154075

[4]: Boutcher SH. High-intensity intermittent exercise and fat loss. J Obes. 2011;2011:868305. doi:10.1155/2011/868305

[5]: Keating SE, Johnson NA, Mielke GI, Coombes JS. A systematic review and meta-analysis of interval training versus moderate-intensity continuous training on body adiposity. Obes Rev. 2017;18(8):943-964. doi:10.1111/obr.12536

[6]: Børsheim E, Bahr R. Effect of Exercise Intensity, Duration and Mode on Post-Exercise Oxygen Consumption. Sport Med. 2003;33(14):1037-1060. doi:10.2165/00007256-200333140-00002

[7]: Laforgia J, Withers RT, Gore CJ. Effects of exercise intensity and duration on the excess post-exercise oxygen consumption. J Sports Sci. 2006;24(12):1247-1264. doi:10.1080/02640410600552064

How accurate is your Garmin’s VO2max estimate?

Posted on by

Traveling along the trails, sidewalks, and main streets of the towns they reside in, runners, cyclists, and endurance sports athletes everywhere all know a familiar sound. The delightfully gratifying chirp of a fitness tracker as you complete your next mile, achieve a new PR (personal record), or record a new VO2max.

Ever since I entered the world of endurance sports training eight years ago, I’ve heard athletes talking about their VO2 max, how to improve it, and how accurate (or not?) fitness trackers are at actually measuring these values.

I decided to explore the technology of Garmin fitness watches to understand how VO2max is calculated and do a baseline comparison of how these wearable technologies VO2max predictions compare to laboratory testing.

Firstbeat Technology’s Fitness Test is used by Garmin and other fitness companies to calculate VO2max for a variety of different activities. Described in patent US20110040193A1, this Fitness Test calculates users’ VO2 in the following steps:

1) The personal background info (at least age) is logged
2) The person starts to exercise with a device that measures heart rate and speed
3) The activity collected data is segmented to different heart rate ranges based off the persons background info and the reliability of different data segments is calculated(reliability is measured based off how continuous the activity is- uninterrupted segments are better than those where the user has to stop)
4) The most reliable data segments are used for estimating the person’s aerobic fitness level (VO2max) by utilizing the person’s heart rate and speed data

Speed data from reliable segments are used to calculate a VO2, oxygen consumption, during that segment. 20-30s bouts are used to calculate VO2 across segments using one of the following theoretical VO2 calculations:

Walking and Pole Walking: Theoretical VO2 (ml/kg/min)=1.78*speed*16.67[tan(inclination)+0.073]
Running on a Level Ground: Theoretical VO2 (ml/kg/min)=3.5 speed
Running in a Hilly Terrain: Theoretical VO2 (ml/kg/min)=3.33*speed+15*tan(inclination)*speed+3.5
Cycling: Theoretical VO2 (ml/kg/min)=(12.35*Power+300)/person’s weight
Rowing (Indoor): Theoretical  VO2 (ml/kg/min)=(14.72*Power+250.39)/person’s weight                                Unit of speed=kilometers per hour (km/h) 
Unit of inclination=degrees)(°) 
Unit of power=watts (W) 
Unit of weight=kilograms (kg)

From these calculated theoretical VO2 values, heart rate information is used to determine effort of segments. Heart rate zones based on user information are utilized to evaluate effort, and then effort is used to determine that VO2 as a %VO2max. VO2max estimates are made for each segment using %VO2max. These segment VO2max can be weighted based off heart beat derived parameters and performance parameters, and then used to calculate VO2max.[1]

An affordable mode of tracking your VO2max through measuring heart rate and speed data – pretty neat, right? But how accurate is this technology and how does it match up to laboratory testing?

Firstbeat conducted their own study to validate the technology and its effectiveness at estimating VO2max. They found that “[t]he accuracy of the method when applied for running is 95% (Mean absolute percentageerror, MAPE ~5%), based on a database of 2690 freely performed runs from 79 runners whose VO2max was tested four times during their 6-9 -month preparation period for a marathon”(4). Error in estimated VO2max was less 3.5ml/kg/min in most cases, which is fairly accurate considering most submaximal testing has an error of 10-15%. Method accuracy varied with respect to estimated maximum heart rate(HRmax). ” If the HRmax is estimated 15 beats/min too low, the error in the VO2max result is about 9%. Respectively, if the HRmax is estimated 15 beats/min too high, the error in VO2max result is 7%. If the person’s real HRmax is known, the VO2max assessment error falls to the 5% level”(5). This study suggests a high degree of accuracy for Firstbeat’s fitness test technology in predicting VO2max.[2]

A group of scientists at Southern Illinois University Edwardsville evaluated the wearable technology’s accuracy by conducting a laboratory VO2max test on male and female runners, then allowing participants to use the wearable technology to calculate VO2max in a 10 minute self guided run. They found that the Garmin Forerunner 230MAX and 235MAX measured VO2max within -0.3 ± 3.4 ml/kg/min, p=0.02 for the 230MAX and -1.1 ± 4.0 ml/kg/min, p=0.026 for the 235MAX for female runners, and -1.1 ± 3.4 ml/kg/min, p=0.149 for the 230MAX and -3.2 ± 4.2 ml/kg/min, p=0.002 for the 235MAX for male runners. There is a greater amount of variability in the male group; however, this could be due to miscalculations in HRmax and potential variations in levels of effort in participant during the 10 minute self guided run. Although there is greater variability within the male group, the devices still appear fairly accurate at predicting VO2max.[3]

Wearable conducted an evaluation of their own putting fitness watches to the test – assessing the accuracy of Garmin, Fitbit, and Jabra devices in measuring VO2max. They found that Garmin technology provided a VO2max estimation within 0.3 ml/kg/min of their study participant, which was the most accurate of all devices tested. The high degree of accuracy found in their study remains consistent with other larger scientific studies.[4]

Across the board, there appears to be a high degree of accuracy with Firstbeat’s Fitness Test in estimating VO2max. For endurance athletes everywhere, this is a huge sigh of relief. Rather than partaking in expensive, strenuous VO2max testing, we can monitor our progress utilizing the technology in the watches we wear everyday. In addition to watching our paces, heart rates, and overall progress, we can also monitor our cardiovascular health and athletic progress as we continue to train and push ourselves everyday.

References:

[1]Seppanen, M., Pulkkenin, A., Kurunmaki, V., Saalasti, S., & Kettunen, J. (2016). U.S. Patent No. US20110040193A1. Washington, DC: U.S. Patent and Trademark Office

[2] Firstbeat Technology(2014). Automated Fitness Level (VO2max) Estimation with Heart Rate and Speed Data.

[3]Snyder, N. C. , Willoughby, C. A. & Smith, B. K. (2017). Accuracy of Garmin and Polar Smart Watches to Predict VO2max. Medicine & Science in Sports & Exercise, 49(5S), 761. doi: 10.1249/01.mss.0000519024.10358.0b.

[4]Stables, J., & Stables, J. (2016, December 21). The big ​VO2 Max test: Fitbit, Garmin and Jabra go head-to-head. Retrieved from https://www.wareable.com/running/best-vo2-max-devices-tested-9129

 

Delayed Onset Muscle Soreness: What We Know and What We Don’t (Emphasis on Don’t)

Posted on by

Ever get that feeling two days after a tough run, or a ride that you knew was just a few miles too long, or your first leg day in months (come on, we’re all guilty of that), where you begin to question whether you will ever walk the same again? Walking down the stairs feels like torture, and your quads feel like they get angrier at you with every step you take? Muscle soreness, more specifically delayed onset muscle soreness (DOMS) is common in athletes of all levels of expertise. It occurs after performing a training activity that is unfamiliar. This could be activities than an athlete has not performed in a few months, activities they’ve never performed before, or even simply an intensity level or duration of exercise that they don’t normally reach, despite performing that exercise regularly. These unfamiliar activities, also known as eccentric training, are known to induce severe muscle soreness characterized by increasing intensity of symptoms beginning as late as 24-48 hours after exercise and lasting for days. The underlying physiological mechanism causing DOMS is still unknown and highly disputed, but at least six hypothesized theories for this mechanism have been proposed: lactic acid, muscle spasm, connective tissue damage, muscle damage, inflammation, and enzyme efflux theories [1]. Currently, there exist therapies that have been experimentally shown to decrease DOMS prevalence, including various hydrotherapies [2] and foam rolling [3], but more effective preventative therapies could probably be developed if the underlying physiological mechanism was identified. In order to better understand this phenomenon and the unfortunate encounters I’m sure we’ve all had with it, we are going to look into some of those proposed mechanisms and try to get some insight on how it works (or doesn’t).

Lactic acid is easy to blame for exercise-related muscle pain because of its high production rates during exercise and its perceived role in muscle fatigue and soreness (which is often highly exaggerated). While lactic acid is a common byproduct of exercise, its role in the development of DOMS is likely insignificant. A study performed in 1983 measuring blood lactic acid concentration before and during two different 45-minute treadmill exercises, one on a level surface and one at a 10% decline, found that DOMS was not prevalent in level-surface runners, even though lactic acid concentration was significantly increased. Conversely, downhill runners saw no significant increases in lactic acid concentrations but experienced significant DOMS [4]. There was clearly no relationship between presence of lactic acid and development of DOMS, and the two in fact appeared to be mutually exclusive, so let’s move on to another of the previously mentioned theories.

The inflammation theory initially seems to have a bit more validity, as the similarities between the acute inflammation response, a response to various types of injury including muscle damage, and DOMS are striking. Both phenomena can be characterized by pain, swelling, and loss of function at the area of interest. The time lines seem to match up as well, as both have been reported to increase in severity for about 48 hours and show signs of healing at 72 hours. The issue with this theory though, is the lack of physiological evidence, which is arguably the most important kind. Studies investigating the relationship between DOMS onset and inflammatory biomarkers, like white blood cells and neutrophils, have often failed to find significant results, leading us to believe that inflammation does not cause DOMS [5]. Another drawback of the inflammation theory is the ineffectiveness of anti-inflammatory drugs in preventing DOMS-related pain. A study done using an anti-inflammatory drug and placebo on athletes undergoing eccentric bicycle exercise found no changes in subjective soreness between drug and placebo groups, suggesting that inflammation is not the source of DOMS pain [6]. We won’t completely remove inflammation from the picture though, as it may play more of a role than it appears.

While inflammation itself is likely not the cause of DOMS pain, inflammatory-related processes may not be completely innocent. Bradykinin, an inflammatory mediator, is believed to play a role in DOMS after a study done in 2010 by Murase et al [7]. This study used a previously established rat model of DOMS to show that injecting a B2 (but not B1) bradykinin receptor antagonist 30 minutes before exercise completely prevented DOMS in those rats. The antagonistic effects of the drug used, HOE 140, only last about an hour in the body, and they found that when injecting it 30 minutes after exercise, it had no effect in preventing DOMS. The results can be seen below.

This suggests that bradykinin released during exercise plays a direct role in the development of DOMS, and that preventing that bradykinin from interacting with the B2 receptor prevents DOMS. The role of bradykinin and the B2 receptor in the development of DOMS is not well understood, but it seems like a step in the right direction to me.

There is too much research out there on DOMS to cover in one lowly blog post. I wanted to debunk the lactic acid theory as lactic acid is often a scapegoat for exercise-related pain that is likely sourced elsewhere. While inflammation and DOMS have many similarities that may lead some to believe that there is a causal relationship there, that is also likely not the case. However, there is definitely evidence of some sort of relationship between the two. Further research into the physiological pathway that leads to DOMS is definitely needed to make any conclusive statements on the issue, and the bradykinin B2 receptor pathway is probably a good place to start. But until then, you’re just going to have to suck it up next time you feel like your quads will never work again two days after your new leg routine. Many have been there and survived before. You will too.

 

Questions to consider:

What distinguishes DOMS from standard muscle soreness?

Think about any times you may have experienced DOMS- what were you doing and why do you think it led to DOMS?

How could you determine the presence of DOMS in animal models when it cannot be subjectively reported? (Hint: check reference 7 for ideas)

How could preventative therapies for DOMS promote better health and wellness?

 

References:

[1] Cheung, K., Hume, P. A., & Maxwell, L. (February 01, 2003). Delayed Onset Muscle Soreness: Treatment Strategies and Performance Factors. Sports Medicine, 33, 2, 145-164.

[2] Vaile, J., Halson, S., Gill, N., & Dawson, B. (March 01, 2008). Effect of hydrotherapy on the signs and symptoms of delayed onset muscle soreness. European Journal of Applied Physiology, 102, 4, 447-455.

[3] Pearcey, G. E., Bradbury-Squires, D. J., Kawamoto, J. E., Drinkwater, E. J., Behm, D. G., & Button, D. C. (January 01, 2015). Foam rolling for delayed-onset muscle soreness and recovery of dynamic performance measures. Journal of Athletic Training, 50, 1, 5-13.

[4] Schwane, J. A., Watrous, B. G., Johnson, S. R., & Armstrong, R. B. (January 01, 1983). Is Lactic Acid Related to Delayed-Onset Muscle Soreness?. The Physician and Sportsmedicine, 11, 3, 124-31.

[5] Smith, L. L. (January 01, 1991). Acute inflammation: the underlying mechanism in delayed onset muscle soreness?. Medicine and Science in Sports and Exercise, 23, 5, 542-51.

[6] Kuipers, H., Keizer, H. A., Verstappen, F. T., & Costill, D. L. (January 01, 1985). Influence of a prostaglandin-inhibiting drug on muscle soreness after eccentric work. International Journal of Sports Medicine, 6, 6, 336-9.

[7] Murase, S., Terazawa, E., Queme, F., Ota, H., Matsuda, T., Hirate, K., Kozaki, Y., … Mizumura, K. (January 01, 2010). Bradykinin and nerve growth factor play pivotal roles in muscular mechanical hyperalgesia after exercise (delayed-onset muscle soreness). The Journal of Neuroscience : the Official Journal of the Society for Neuroscience, 30, 10, 3752-61.