Identify
I am sure most of you are familiar with the term Body Mass Index (BMI), and some of you may have even received one. Also, I am sure most of you are familiar with the controversy regarding the accuracy of BMIs. Unfortunately, BMI results do not accurately reflect the body fat percentage of certain populations, such as athletes and the elderly, because muscle mass is not taken into account [1]. For example, an athlete with significant muscle mass would report as overweight and an older individual lacking muscle mass would report as underweight [1]. In hopes of correcting the inaccuracies stemming from BMI calculations, bioelectrical impedance analysis (BIA) became a popular method for measuring body fat mass and body fat percentage.
With BIA, a small, alternating current is sent throughout the body and the impedance of electrical current to fat, water, and muscle content is recorded [2]. Fattier tissues will reduce the speed of electrical current whereas hydrated and muscular tissues will not [3]. Assuming that the body exists as a conductive cylinder uniform in material and density, allows for these impedance measurements to be easily converted into body composition measurements [4]. However, due to these assumptions, inaccuracies persist and an advantage of BIA over BMI remains unclear. BIA has the potential of providing more accurate and reliable results, but that must start with correcting the issues that result from its assumptions, more specifically its assumption that the body exists as a conductive cylinder.
Preliminary bioelectrical impedance analyzers made use of a one-cylinder model to make body composition measurements [5]. Unfortunately this method led to the underestimation of total body water, thus, leading to inaccurate results of body fat mass and lean body mass (Figure 1) [5]. To improve upon this issue, the 5-cylinder model was developed which makes cylinders out of the arms, legs, and trunk (Figure 1) [5]. In addition, the 5-cylinder model was able to expand upon its predecessor by providing detailed reports of each body part’s composition and whole-body composition [5].
In Calculus we learned that when approximating the area under the curve our estimation yields better results when we add more rectangles with smaller widths. Analogous to the previous scenario, our body composition measurements would prove to be more accurate by increasing the number of cylinders our body could model. Instead of using one cylinder, it may be more beneficial to have 5 cylinders.Formulate
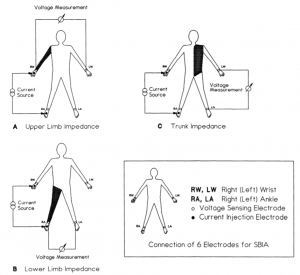
To measure impedance among 5 cylinders requires more electrodes than the four that come with conventional BIA (Figure 2) [6]. Moreover, for the 5-cylinder model, all alternating current is supplied between the right ankle and right wrist [6]. To measure the potential difference of the upper limbs, lower limbs, and trunk, the electrodes are placed between the right and left wrist, right and left ankle, and left ankle and wrist, respectively [6]. All electrodes pairs are then attached to a four-channel, battery operated impedance instrument that reports the resistance, reactance, phase angle, and impedance [6].
In order to calculate impedance, the resistance, R, reactance, Xc, and phase angle must be known (Equation 1) [7]. Resistance is reflective of electrolyte-containing total body water in which lean muscles tend to have low resistance and fattier tissues tend to have a high resistance [7]. Reactance is reflective of body cell mass in which a higher proportion of cells gives rise to low reactance and a lower proportion of cells gives rise to a high reactance [7]. The phase angle readout is a component of the impedance instrument that allows for differentiation between resistance and reactance [7].Z^2 = R^2 + Xc^2 Equation 1
Now that we know how to calculate impedance, we must now relate impedance to total body water (TBW) shown in Equation 2 [6].
TBW = L^2/Z Equation 2
L: length of cylinder
Z: impedance of cylinder
To make use of these equations while maintaining full transparency, we must clarify the assumptions. Therefore, we assume:
- The supplied current follows the path of least resistance.
- The body is made up of segmental conductive cylinders [6].
- The total body water occupies a cylinder of length, L, and is uniform in resistivity (Equation 2) [6].
By assuming the path of least resistance we can exclude extraneous and complex equations that would otherwise be needed to solve for resistance. Secondly, by assuming segmental conductive cylinders, we can analyze a body part’s contribution to whole body impedance. Lastly, by assuming what is shown in Equation 2 we can again exclude extraneous and complex equations that would otherwise be needed to solve for TBW.
Solve
With this segmented approach, we can better estimate lean body mass (LBM) and fat mass (FM) by recording the individual lengths and resistivities of upper limb, lower limb, and trunk cylinders (Equation 3). Whereas for a one-cylinder model, the entire body was assumed to have one resistivity, which is inherently untrue considering the trunk and limbs distribute lean muscle and fat differently [6]. Unfortunately, even through a segmented approach of solving for TBW, reliability of Equation 2 is questionable which continues into Equation 3 [6]. Studies have shown that impedance, Z, contributes little to solving for lean body mass (LBM). Moreover, changes in impedance showed little to no change in LBM [6].
TBW = Lᵤₗ^2/Zᵤₗ + Lₗₗ^2/Zₗₗ + Lₜ^2/Zₜ Equation 3
ul: upper limb
ll: lower limb
t: trunk
Despite its reliability being under question, we continue to make use of assumptions to simplify equations while maintaining some degree of accuracy. Moreover, now that we know TBW, we can solve for LBM and fat mass (FM) through the empirical estimations shown in Equation 5 and Equation 4 [7]. These empirical estimations are based on observations of human biological phenomena where on average a human’s lean body mass contains 73% of their total body water [7]. Because we are not all the same, deviations from Equation 4 do exist, which is a limitation of using empirical calculations.
LBM = TBW/0.73 Equation 4
FM = Body Mass – LBM Equation 5
Although the segmental approach improves accuracy in comparison to the one-cylinder model, discrepancies still exist through the use of assumptions and empirical estimations. To further improve upon BIA, it is important that we rid of all empirical estimations and analyze impedance solely on the person. Fortunately, companies like InBody have made strides in improving this technology by minimizing the use of empirical estimations [5].
References
- Assessing Your Weight and Health Risk. NIH. Website. https://www.nhlbi.nih.gov/health/educational/lose_wt/risk.htm. Accessed May 1, 2020.
- Grossi, M., Ricco, B. Electrical impedance spectroscopy (EIS) for biological analysis and food characterization: a review. J Sens Sens Syst. 2017; 6: 303-325. https://doi.org/10.5194/jsss-6-303-2017.
- Bioelectrical Impedance Analysis (BIA). Science for Sport. Website. https://www.scienceforsport.com/bioelectrical-impedance-analysis-bia/. Published May 20, 2018. Accessed February 27, 2020.
- Dehghan, M., Merchant A.T. Is bioelectrical impedance accurate for use in large epidemiological studies? Nutr J. 2008; 7: 36. doi: 10.1186/1475-2891-7-26
- Revolutionizing BIA Technology with InBody. InBody. Website. https://inbodyusa.com/general/technology/. Accessed May 12, 2020.
- Organ LW, Bradham GB, Gore DT, Lozier SL. Segmental bioelectrical impedance analysis: theory and application of a new technique. Journal of Applied Physiology. 1994 Jul; 77(1): 98-112.
- Bioelectrical Impedance Analysis (BIA) and Body Composition Analyse. DANTEST Media Inc. Website. http://www.dantest.com/dtr_bioscan_bia.htm. Accessed May 12, 2020.