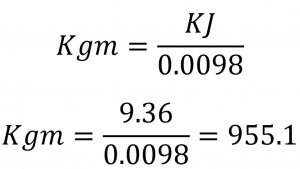Monark Ergometer 879E [3] Monrk Ergomedic 839E [6]
IDENTIFY
The basic principle of any ergometers is to measure the distance traveled in relation to an applied force to output the work that has taken to perform that task. This work outuput can be used to determine how much power has been produced and how much metabolic energy has been consumed [1]. Cycle ergometers are a common type of ergometers used for cardio-pulmonary exercieses and sports medicince diagnostic and performance testing which uses the task of cycling. When designing a cycle ergometer for repeated exercise usage it is improtant to think about what are the key components of the machine, the intended usage, how closely the machine can simulate road bike cyclig, storage, and the impact of that the device can have on the user and their exercice. An engineering problem in designing a cycle ergometer is determining the optimal size of key components like the wheel and thus the overall machine.
The motivation for this is that a smaller wheel allows for the machine to be more compact, lighter, and more portable allowing for greater home or clinical use
The unknown being solve for is the size of the wheel since this will give a known distance that the user has “travelled” per revolution and thus the equation for work (Work = Force*Distance) can be applied to find the unknown. The wheel is the main component of a cycle ergometer machine since it is the component that is being used to measure work output. Determining the optimized size of this wheel allows for adjecent compoenets to be appropriately designed so that the cycle ergometer is as compact as possible but still fully functional.
Question: Find the minimum diameter that the wheel can be in order to power the cycle ergometer at max applied force
FORMULATE
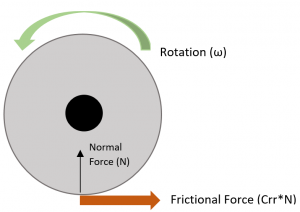
Figures:
Fig 1: Assumed forces acting on the wheel of the cycle ergometer
Background: Knowing what the minimum input wattage it takes to power the cycle ergometer, it is possible to use the conversion relationships for wattage and Kilojoules and Kilojoules and work to convert wattage into the minimum workout output needed to power the machine [1]. Knowing this then the equation for work can be used to determine the circumference and thus the diameter that the wheel needs to be.
Assumptions: the main wheel of the machine is a disc wheel with a mass of: 1.1Kg [2]
Based on previous cycle ergometer models the minimum power needed to power on the machine is: 156W at 60rmp [3]
The max applied force based on previous cycle ergometer models is: 12Kg [3]
The coefficient of rolling resistance (Crr) based on production bike tires at 31mph measured on rollers is: 0.005 [4]
Equations:
Unknowns: kilojoules (KJ), work (Kgm), wheel circumference (D), wheel diameter (d)
Knowns: Watt = 8W, seconds = 60s, coefficient of rolling resistance (Crr) = 0.005, Normal force (N) = 1.1Kg, applied force (F) = 12Kg, x = 60 rpm, time (t) = 1min
SOLVE
The first step in solving this problem is converting the minimum power input from Watts into Kilojoules so that it can be converted into the units for work.
Now that the kilojoules has been determined, the minimum input power can be converted into the units for work based on the relationship for kilograms per meter (Kgm) and kilojoules (KJ).
Since we now know the minimum work it takes to power the cycle ergometer, we can apply the equation for work to determine the circumference of the wheel.
We now have obtained the circumference of the wheel, yay! The final step in determining the optimal size and the answer to the question is to convert the circumference into diameter as follows:
From the calculations the minimum the wheel can be to power the machine at max applied force is 0.423m. This result is slightly smaller than the current common road bike wheel size of 0.7m in diameter [5] but still within a resonable range. This could be due to the impact of the assumptions made. It was assumed that the wheel of the cycle ergometer is a disc wheel which tends to be ligter than normal road bike wheels. It was also assumed that the coeficient of rolling resistance (Crr) was relatively high due to the assumed contact of adjacent component, which could impact the size since a smaller wheel takes less work to overcome the same rolling resistance as a larger wheel. Some limitations to this process are that it does not take into account of other acting forces other than applied force and rolling friction while also assuming that the user can cycle a minimum of 60rpm when this typically not physiologically possible for the typical user. While the calculated diameter is relatively smaller than current commercial road bike wheel, the calculated diameter is whithin a resonable range and so it can be concluded that the minimum wheel diameter needed to power a cycle ergometer at max applied force is 0.423m.
References:
- Egometer powerpoint by Dr. Robert Robergs at UNM
- Disc wheels at cyclinguphill.com
- Monark Egometer 874E Manual, Monark Exercise AB
- Rolling Resistances, Wikipedia
- Common Tire Sizes at biketiresdirect.com
- Monark Ergomedic 839E Manual, Monark Sports and Medicine
